Introduction

Thermodynamic, hydrodynamic and non-linear modeling often requires thermodynamic derivatives, therefore IAPWS_IF97 can calculate most property derivatives as functions of pressure and enthalpy, e.g.: dT/dp_ph, cp_ph, dv/dp_ph and dv/dh_ph. Since modeling often involves multiple dimensions that are discretized or meshed to form a set of either finite-difference or finite-element equations, IAPWS_IF97 is vectorized even across regions (subcooled/compressed-liquid, saturated, superheated and supercritical). It is fully validated against the IAPWS_IF97 standard test and is over 10X faster than XSteam-2.6.

Installation

Download IAPWS_IF97 from the MATLAB Central File Exchange, place on your path and use!

IAPWS_IF97 Standalone Function with No Slip

IAPWS_IF97 is 27 basic water functions of water properties, based on the International Association on Properties of Water and Steam Industrial Formulation 1997 (IAPWS-IF97), IAPWS-IF97-S01, IAPWS-IF97-S03rev, IAPWS-IF97-S04, IAPWS-IF97-S05, Revised Advisory Note No. 3 Thermodynamic Derivatives from IAPWS formulations 2008, Release on the IAPWS Formulation 2008 for the Viscosity of Ordinary Water Substance, 2008 Revised Release on the IAPWS Formulation 1985 for the Thermal Conductivity of Ordinary Water Substance.

Usage

IAPWS_IF97(FUN,IN1,IN2)

FUN is the desired function that may take 1 input, IN1, or 2 inputs, IN1 and IN2. IN1 and IN2 can be scalar, column vector or matrix, and IN1 and IN2 should be the same size. If a row vector is entered, it is transposed. If a scalar is entered for one input and the other input is a vector or matrix, then the scalar is repeated to form a vector or matrix of the same size as the other input.

FUN is a string that is formed by the property symbol, an underscore and the property symbols the function depends on. EG: ‘k_pT’ is thermal conductivity, ‘k’, as a function of pressure, ‘p’, and temperature, ‘T’. Derivatives are formed by prefixing ‘d’ to the property symbol and suffixing ‘d’ + the property symbol to which the derivative is with respect. EG: ‘dTdp_ph’ is the derivative of temperature with respect to pressure as a function of pressure and enthalpy, ‘h’, at constant enthalpy. The exception to this rule is ‘cp_ph’ which is equivalent to ‘1/dTdh_ph’ or the reciprocal of the derivative of temperature with respect to enthalpy as a function of pressure and enthalpy at constant pressure. All derivatives are with respect to pressure at constant enthalpy or v.v.

Saturation is indicated by suffixing ‘sat’, saturated liquid ‘L’ and saturated vapor ‘V’.

FUN = [d]<property-symbol>[sat|L|V][d<property-symbol>]_<property-symbol>...

Property Symbols:

p [MPa] pressure
T [K] temperature
h [kJ/kg] enthalpy
v [m^3/kg] specific volume the reciprocal of density, IE: v = 1/rho
x quality, mass fraction of liquid water in mixture
k [W/m/K] thermal conductivity
mu [Pa*s] viscosity
cp [kJ/kg/K] specific heat at constant pressure

Basic functions: h_pT, v_pT, vL_p, vV_p, hL_p, hV_p, T_ph, v_ph, k_pT, k_ph, mu_pT, mu_ph, dhLdp_p, dhVdp_p, dvdp_ph, dvdh_ph, dTdp_ph, cp_ph, dmudh_ph, dmudp_ph, psat_T, Tsat_p, dTsatdpsat_p, x_ph, x_hT, x_pv, x_vT

Example:

>> press_rng = logspace(-2,2,300);  [MPa] pressure (p) range
>> temp_rng = 273.15+linspace(1,800,300);  [K] temperature (T) range
>> [p,T] = meshgrid(press_rng,temp_rng);  [MPa,K] mesh p & T
>> h = IAPWS_IF97('h_pT',p,T);  [kJ/kg] enthalpy = f(p,T)
>> psat = IAPWS_IF97('psat_T',temp_rng);  [MPa] saturation pressure
>> psat = psat(~isnan(psat));  trim out of range temperatures
>> hLsat = IAPWS_IF97('hL_p',psat);  [kJ/kg] saturated liquid enthalpy
>> hVsat = IAPWS_IF97('hV_p',psat);  [kJ/kg] saturated vapor enthalpy
>> pcrit = 22.064;  [MPa] critical pressure
>> hLcrit = IAPWS_IF97('hL_p',pcrit);hVcrit = IAPWS_IF97('hV_p',pcrit);
>> Tcrit = IAPWS_IF97('Tsat_p',pcrit); hcrit = IAPWS_IF97('h_pT',pcrit,Tcrit);
>> hVL = hVsat - hLsat;  [kJ/kg] heat of vaporization
>> hX = hLsat*ones(1,9) + hVL*(0.1:0.1:0.9);  [kJ/kg] mixture enthalpy

Pressure-Enthalpy Diagram

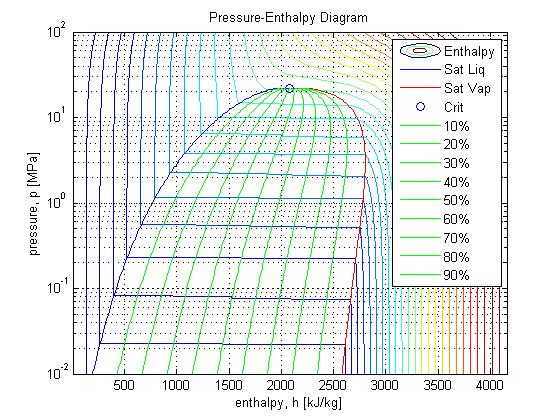
Reference: Revised IAPWS Industrial Formulation 1997